Teorema de Tales
O Teorema de Tales é um princípio da geometria que afirma que existem segmentos proporcionais presentes em um feixe de retas paralelas, quando cortado por retas transversais.
Esse teorema foi criado por Tales de Mileto, um importante matemático, filósofo e astrônomo grego que ao observar as sombras de uma pirâmide, encontrou proporcionalidade entre a medida dessas sombras e a altura da pirâmide.
Passo a passo para a interpretação do Teorema de Tales
Para que você entenda melhor o conceito do Teorema de Tales, precisa levar em consideração as seguintes informações:
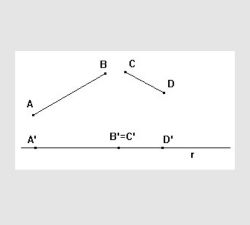
- Um feixe de retas paralelas são 3 ou mais retas dispostas paralelamente, como no exemplo abaixo;

- Uma reta transversal é a linha que corta retas paralelas, como a reta t da imagem abaixo;

- Um segmento de reta é a parte de uma reta determinada por dois pontos. Os segmentos da reta r da imagem abaixo são: AB, CD e o segmento maior AD;
- A razão designa a comparação entre duas grandezas. Atente-se ao exemplo:
Se em um problema matemático você possui as grandezas 60 e 20, qual será a razão entre elas? Para descobrir, aplique:

A razão entre as grandezas 60 e 20 é 3.
Atenção: dentro da razão existe uma grandeza que será antecedente (numerador) e outra consequente (denominador). Para descobrir a posição de cada uma esteja sempre atento ao enunciado da questão ou às informações disponibilizadas.
- Proporção é quando duas razões são iguais;
Todo esse passo a passo nas informações acima são importantes para você entender e analisar um Teorema de Tales. No exemplo abaixo, entenda como funciona o conceito de proporção de retas.
Exemplo de Teorema de Tales
Na imagem abaixo, podemos avaliar um Teorema de Tales. Veja que ele contém um feixe 3 de retas (a,b e c), 2 retas transversais (r e r'), e alguns segmentos de reta, como o AB ou A'C'.
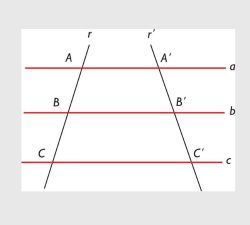
O que o torna um Teorema de Tales é os segmentos de retas presentes na imagem são proporcionais. Para descobrir isso, temos que constatar se as razões presentes são proporcionais. Na imagem acima, por exemplo, podemos ver que:
{A\B = A’\B’} e {B\C = B’\C’}
Lê-se:
- O segmento de reta A\B é proporcional ao segmento de reta A’\B’, já que suas razões são iguais.
- O segmento de reta B\C é proporcional ao segmento de reta B’\C’, já que suas razões também são iguais.
Esses não são os únicos segmentos proporcionais dentro do teorema. Também é possível encontrar a seguinte razão:
{A\C = A’\C’}
Neste caso, lê-se:
- O segmento de reta A\C é proporcional ao segmento de reta A'\B', já que suas razões são iguais.
Exemplo de Teorema de Tales nos triângulos
O Teorema de tales também pode ser aplicado em situações com triângulos. Na imagem abaixo, por exemplo, pode-se concluir que:
- Os segmentos de retas DE e BC são proporcionais.
- Logo, podemos os triângulos ABC e ADE também são proporcionais.

Neste caso, representa-se da seguinte maneira:
Δ ABC ~ Δ AED
Veja também o significado de:





