Soma e Produto nas Equações do 2ª Grau
Soma e Produto é um método aplicado em equações do 2º grau para encontrar as suas respectivas raízes.
O método da soma e produto costuma ser usado como uma alternativa à Fórmula de Bhaskara, por consistir em uma técnica mais simples e rápida de obter os resultados pretendidos.
No entanto, a aplicação da soma e produto em uma equação do 2º grau é aconselhada apenas quando os coeficientes desta são números inteiros. Caso sejam fracionados, por exemplo, o esquema de Bhaskara poderá ser mais fácil.
Como usar o método da soma e produto
Para usar essa técnica é preciso aplicar duas fórmulas distintas:
Soma das raízes
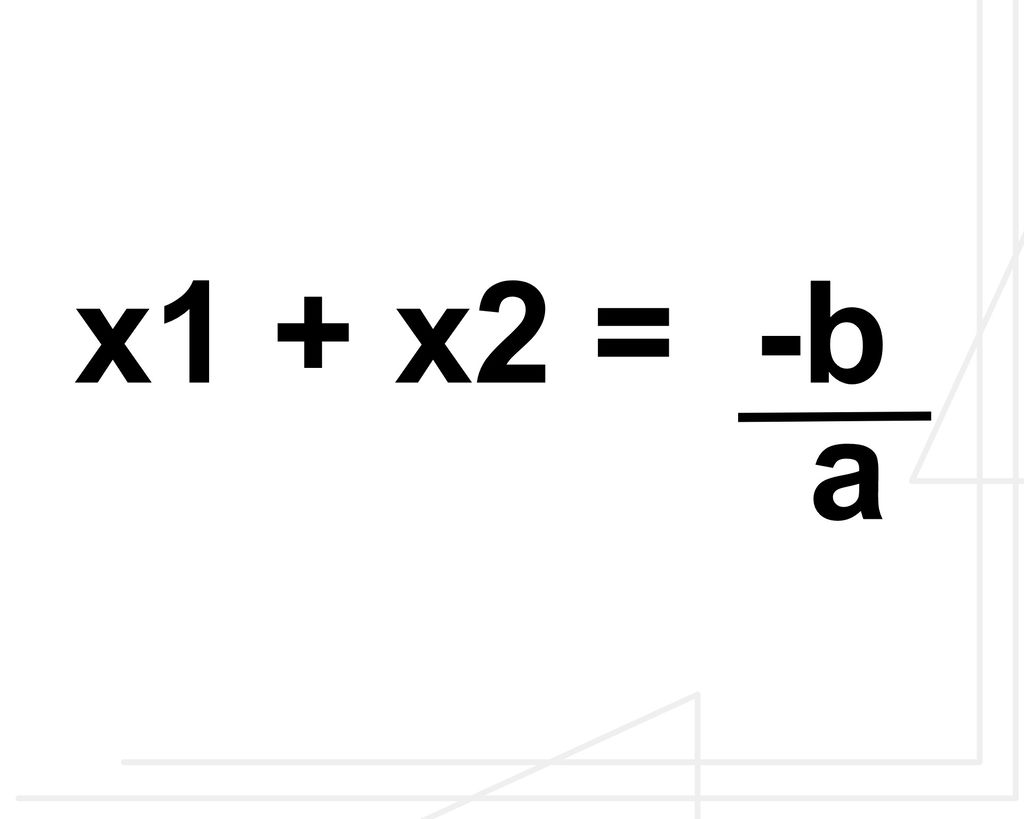
Produto das raízes
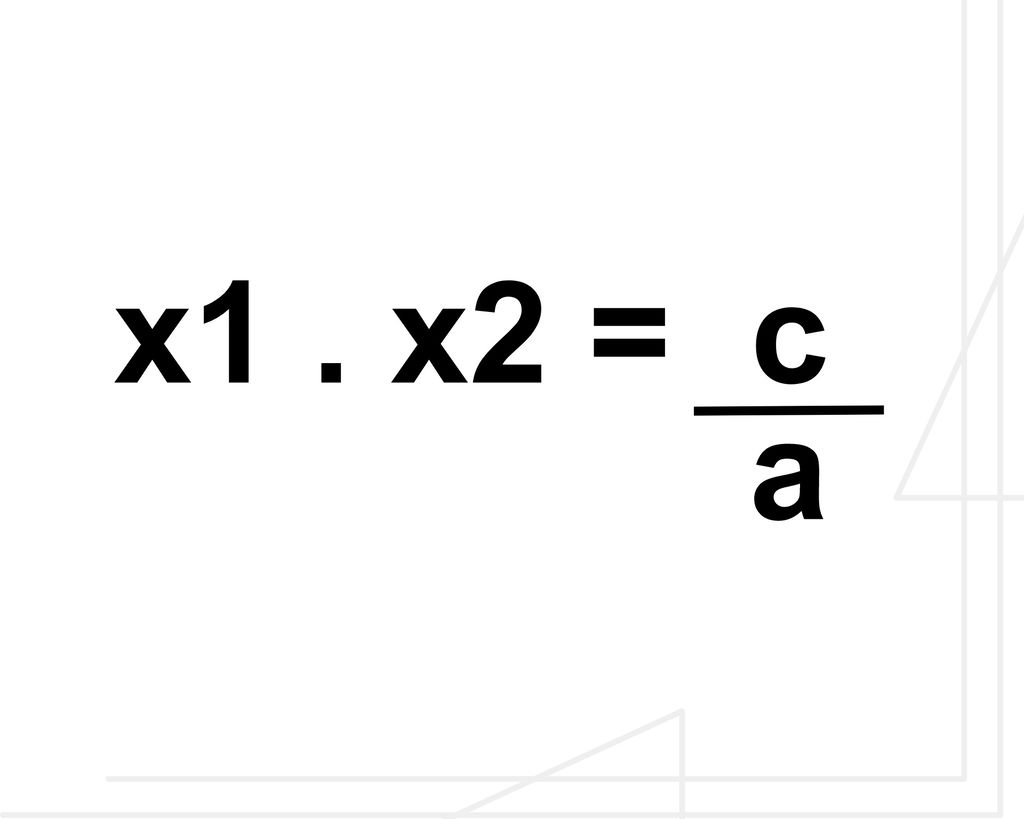
Essas fórmulas são extraídas da própria fórmula de Bhaskara, onde as raízes são obtidas por:
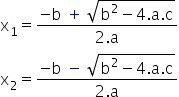
As fórmulas de soma e produto são uma maneira simplificada de encontrar as raízes (x1 e x2) a partir de a, b e c, sem precisar realizar todo o cálculo de Bhaskara.
Antes de começar o cálculo das raízes é preciso lembrar da forma como a equação do 2º grau precisa ser escrita:
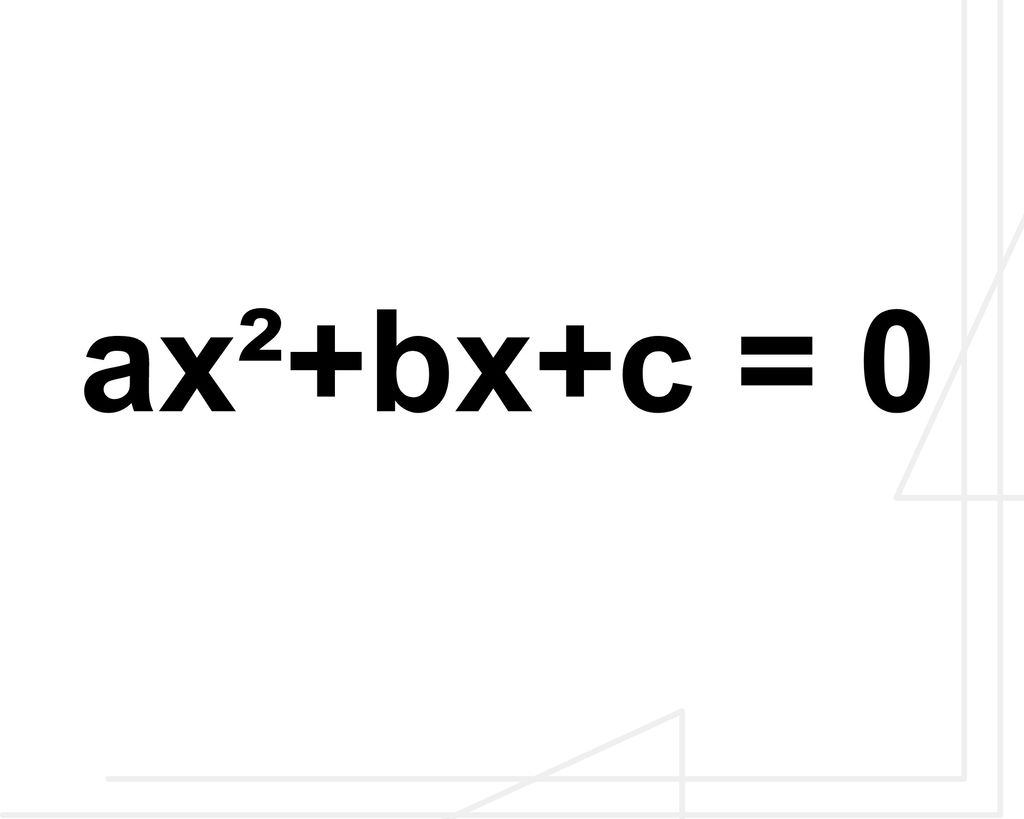
E então é só substituir as letras (a, b e c) pelos números, conforme a posição em que estão. Veja nos exemplos a seguir:
Exemplo 1 de soma e produto das raízes
Na equação de 2° grau: x2 - 7x + 10 = 0, para descobrir a soma das raízes, primeiro se observa que a é igual a 1 (pois não há nenhum número à frente do x2). O b corresponde a -7 e c ao 10.
Ao se identificar a, b e c, aplica-se a fórmula da soma das raízes: x1 + x2 = -b/a. Assim, -b/a é igual a -(-7)/1. Observe o cálculo abaixo:
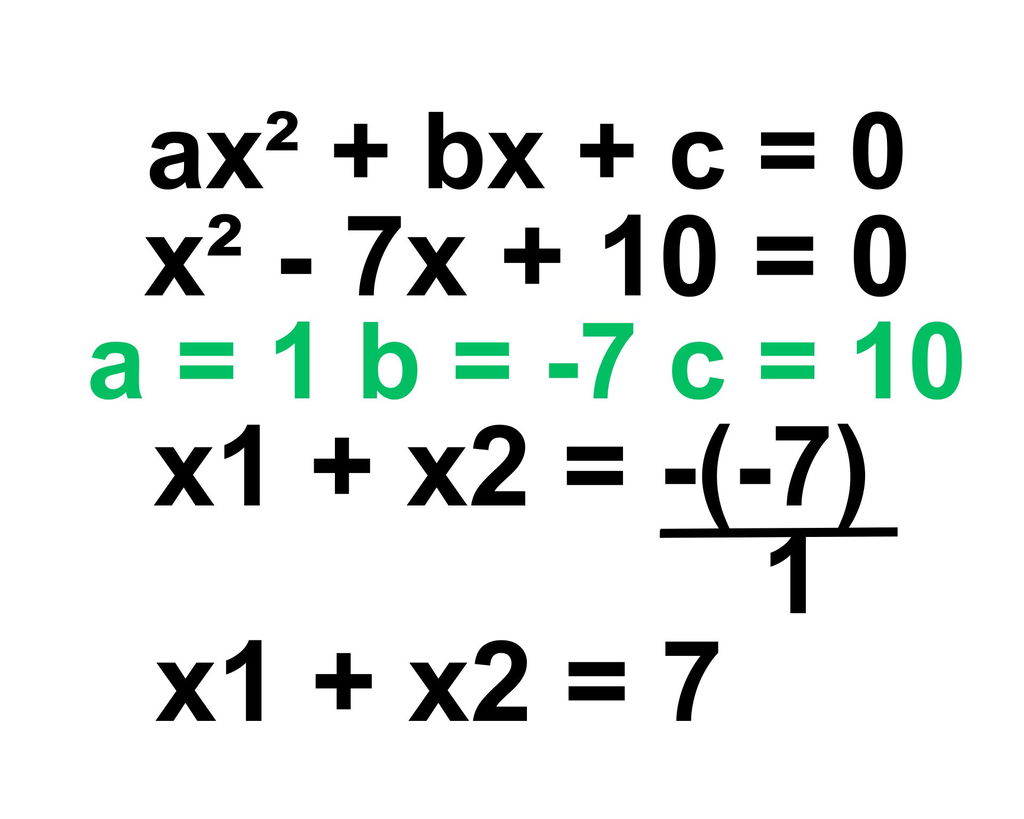
Dessa forma, descobre-se que x1+ x2 é igual 7. É importante sempre ter atenção aos sinais de + e -. Como a fórmula é -b/a e o número 7 já era negativo, vai para dentro dos parênteses: -(-7). Os dois sinais de menos (-) resultam em mais (+).
No produto das raízes o mesmo deve ser feito, mas usando a fórmula do produto: x1. x2 = c/a. Veja o cálculo:
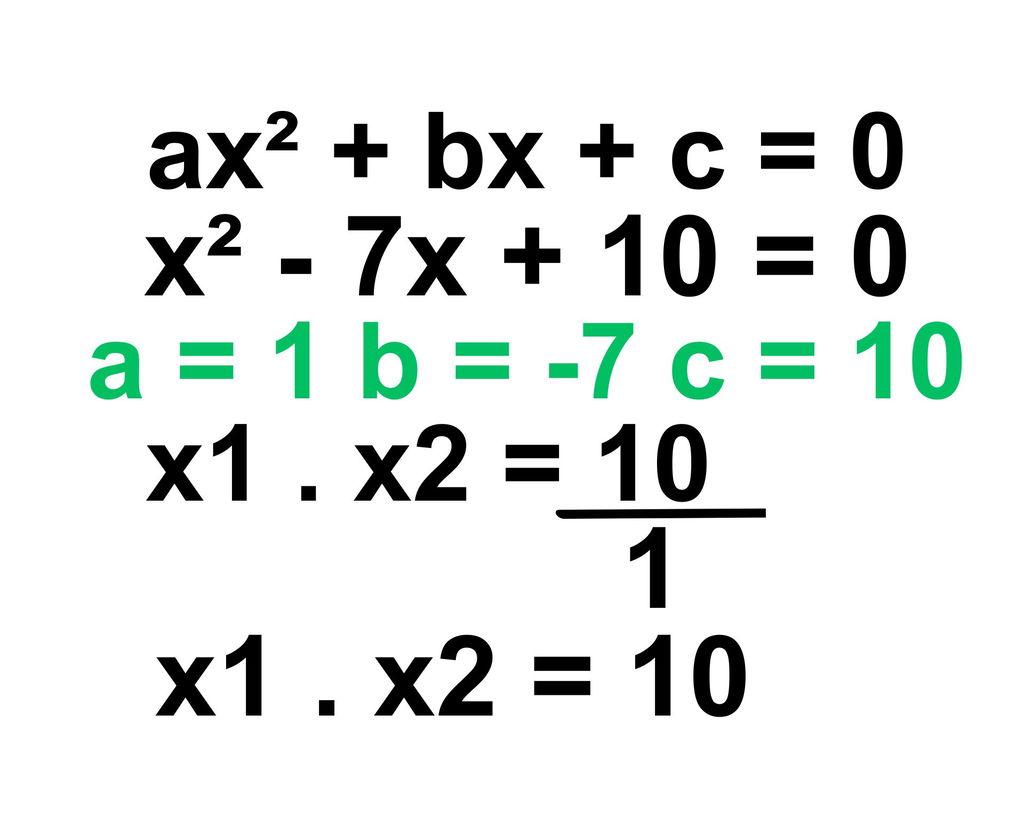
Tem-se a igual a 1 e c igual a 10, por isso, x1. x2 é igual a 10. Feitos esses dois cálculos iniciais, para descobrir a soma e o produto das raízes, é preciso encontrar dois números que somados deem 7 e que multiplicados resultem em 10. Assim, descobre-se o valor de x1 e x2, individualmente.
Pode-se começar pelo resultado do produto, já que pode ser mais simples encontrar números que multiplicados resultem no valor calculado. Se fosse iniciado pela soma, as hipóteses seriam maiores e as contas mais demoradas.
Tendo x1. x2 = 10, pergunta-se: quais números multiplicados um pelo outros têm como o resultado 10? Pode dizer que 1 . 10 = 10 e 2 . 5 = 10. Tem-se, então, como hipóteses 1, 10, 2 e 5.
Passamos então para a soma, dos números das hipóteses definidas no cálculo do produto, quais deles quando somados dão como resultado 7? Entre as opções disponíveis, comprova-se que 2 e 5 são os resultados corretos, já que 2 + 5 = 7.
Desta forma, descobre-se que as raízes da equação são x1 = 2 e x2 = 5.
Conheça também a tabuada completa e tipos de triângulos.
Exemplo 2 de soma e produto das raízes
Na equação x2 − 5x + 6 = 0, qual será o valor de x1 e x2? Começa-se pela soma das raízes: x1+ x2 = -b/a, em que b é igual -5 e a é igual a 1. Acompanhe o cálculo:
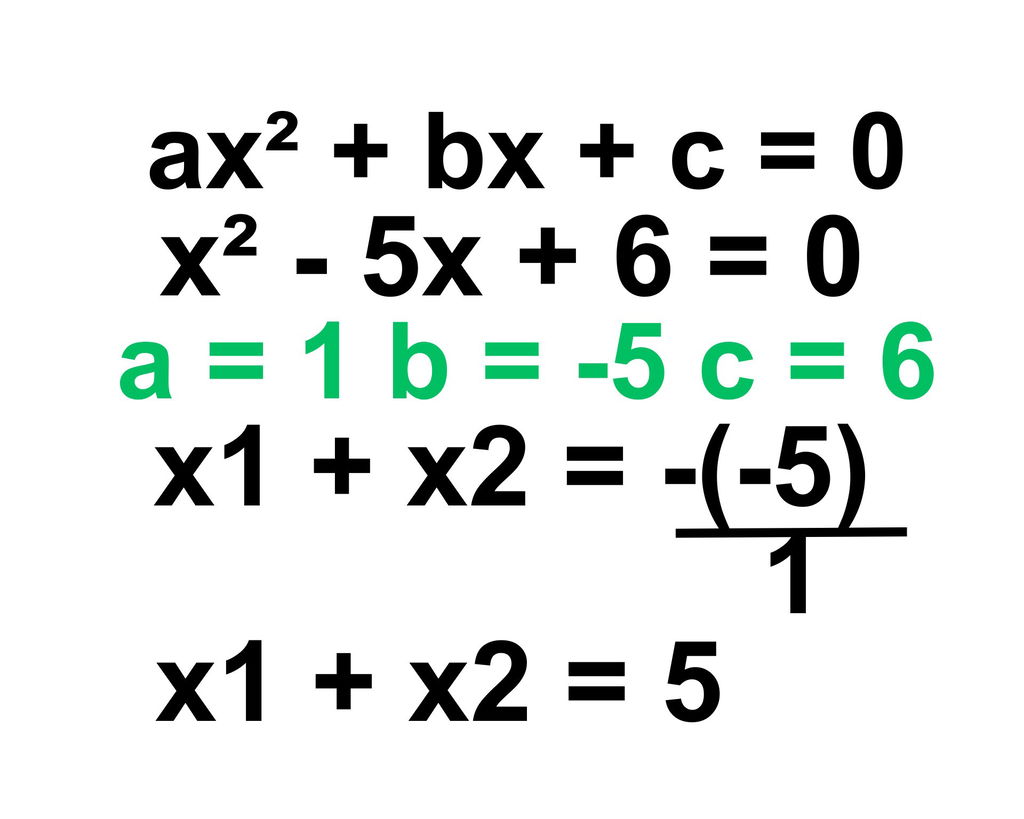
No produto das raízes, partimos da fórmula x1 . x2 = c/a, sendo c igual a 6 e a igual a 1. Veja o cálculo:
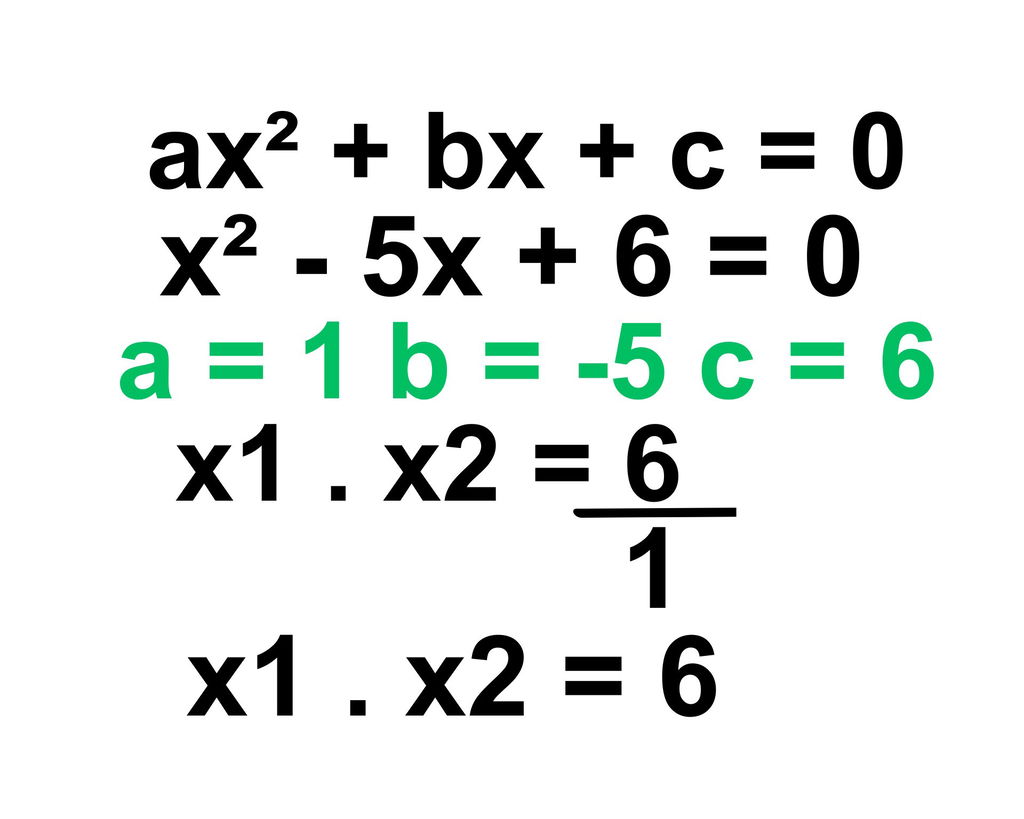
Sabendo que x1 + x2 é igual a 5 e, x1. x2 resulta em 6, devemos pensar: quais números multiplicados têm como resultado 6? Tem-se 6. 1 = 6 e 2. 3 = 6. Então, as hipóteses são 1,6,2 e 3.
Dentre esses números, quais deles somados têm como resultado 5? O 2 e o 3, pois 2 + 3 = 5, logo x1 = 2 e x2 = 3.
Quando o método da soma e produto deve ser aplicado
Nem todas as equações do 2º grau permitirão a aplicação do método da soma e produto. Caso não seja possível, muito difícil ou mais demorado encontrar dois números que satisfaçam as fórmulas de soma e de produto, será necessário resolver o cálculo usando a fórmula de Bhaskara.
Por exemplo, a equação do 2º grau: x2 + 3x + 5 = 0. O cálculo da soma das raízes será, resumidamente: x1 + x2 = -3/1 = -3. Já a conta do produto das raízes será: x1 . x2 = 5/1 = 5.
Neste caso, ao tentar encontrar os números que multiplicados resultem em 5, teremos somente 5 e 1, pois 5 . 1 = 5. Porém, a soma desses dois algarismos é diferente de -3. Assim, é impossível determinar as raízes da equação através do método da soma e produto, devendo-se usar Bhaskara.
Veja também como calcular a fórmula de Bháskara, teorema de Pitágoras e regra de 3.
