Probabilidade
A probabilidade é um campo da matemática que estuda as chances de ocorrência de um evento em um experimento aleatório.
É utilizada para calcular as chances de determinado resultado, como no lançamento de um dado ou mesmo nas chances de alguém ganhar a loteria.
A probabilidade matemática é representada pelo conjunto de números entre 0 e 1:
- Quando um evento tem probabilidade 0, sua ocorrência é impossível,
- Quando a probabilidade de um evento é 1, este evento acontecerá com certeza.
Como calcular a probabilidade?
Para calcular a probabilidade, divide-se o número de ocorrências do evento que se espera pelo número de total de eventos possíveis. Por exemplo, se calcularmos a probabilidade de uma moeda lançada ao chão cair com a face coroa virada para cima, teremos:
- Uma (1) possibilidade de ocorrência do evento que desejamos: coroa,
- Duas (2) possibilidades de eventos totais: cara e coroa.
Assim, teremos a probabilidade de "coroa" de 1/2 ou 50%.
Fórmula da probabilidade
Para compreender melhor como calcular a probabilidade, observe a fórmula:
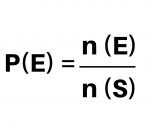
Onde:
- P(E) = probabilidade da ocorrência de um evento E
- n(E) = número total da ocorrência do evento E
- n(S) = número de ocorrência do espaço amostral S
Antes de ver exemplos práticos de cálculos, entenda alguns conceitos fundamentais da probabilidade:
Experimento aleatório
A probabilidade somente poderá ser calculada nos casos de experimentos aleatórios, isto é, nas situações em que não é possível determinar ou prever o resultado.
Um dos exemplos de experimento aleatório é o lançamento de um dado. Se o dado não estiver viciado (com mais peso em uma das faces, por exemplo), não é possível determinar qual face cairá virada para cima, isto é, o resultado do lançamento depende do acaso.
Outro exemplo seria uma sacola cheia de bolas azuis e amarelas de mesmo tamanho e peso. Ao escolher uma das bolas ao acaso, sem vê-las, não há como saber se sairá uma bola azul ou amarela, assim, este experimento é aleatório.
Espaço amostral
O espaço amostral é o conjunto de todos os resultados possíveis em um experimento aleatório. Por exemplo, quando lançamos um dado, o espaço amostral (S) é representado por todos os valores do dado, isto é: (S) = {1,2,3,4,5,6}.
O espaço amostral, então, é o conjunto de todas as faces do dado, pois as 6 faces são as 6 possibilidades de acontecerem após um lançamento. Assim, apesar de não ser possível prever o resultado, sabemos que ele estará dentro do espaço amostral.
Evento
O evento (E) é um subconjunto do espaço amostral (S). Ao lançar um dado, pode-se determinar como evento a ocorrência do número 5, E = {5} ou então de um número par, E = {2,4,6}.
Tipos de eventos
- Evento certo: é aquele que representa o próprio espaço amostral (E = S) e acontecerá com toda certeza. Após o lançamento de um dado padrão (com números de 1 a 6), a chance de sair um número natural é 100%, pois todos os números de 1 a 6 são naturais.
- Evento impossível: é aquele que tem 0% de chances de acontecer. Ao lançar um dado padrão, a chance de sair o número 8 é zero, pois o dado não possui nenhuma face com o número 8.
- Eventos complementares: são aqueles em que a intersecção entre os eventos é representada por um conjunto vazio e a união é representada pelo conjunto amostral inteiro.
A probabilidade de ocorrência de um número par e de um número ímpar no lançamento de um dado são eventos complementares. Pois, o somatório das ocorrências desses dois eventos é representado pelas 6 possibilidades: E = {1,2,3,4,5,6}.
Nesse caso não haverá intersecção, pois um número não pode ser par e ímpar ao mesmo tempo.

Exemplos de exercícios de probabilidade
Vamos exercitar o uso da fórmula de probabilidade com um exemplo:
- Ao lançar um dado, qual a probabilidade da ocorrência dos seguintes eventos:
a) Número ímpar:
Exitem três possibilidades de sair um número ímpar: E = {1,3,5}. Nesse caso, n(E) = 3. Sendo o número total de possibilidades n(S) = 6, temos:

Nesse caso, há 50% de chances de sair um número ímpar.
b) Número 5:
Só existe uma possibilidade de sair o número 5, assim n(E) = 1. Considerando o total de possibilidades n(S) = 6, temos:
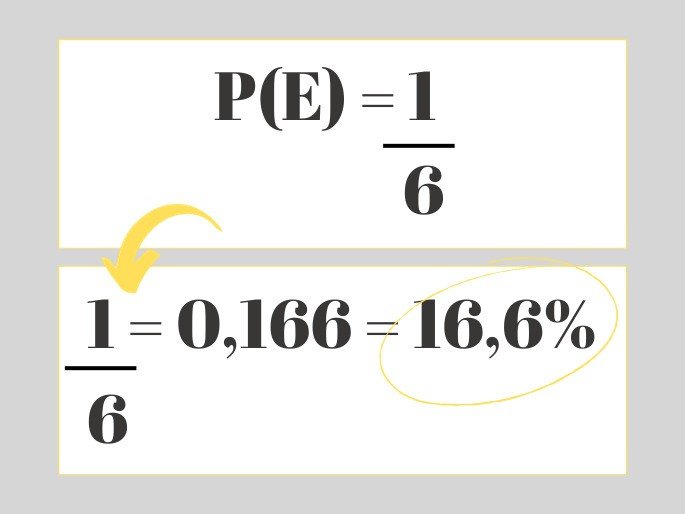
Nesse caso, há, aproximadamente, 16,6% de chance de sair o número 5 ao lançar um dado.
Observe que, como dissemos no início do texto, a probabilidade sempre será um número entre 0 e 1, onde 1 representa 100% de chance da ocorrência de um evento e 0, a impossibilidade de ocorrência do evento.
Veja também o significado de aritmética, porcentagem e geometria.