Porcentagem (%)
Porcentagem ou percentagem é uma área da matemática que indica uma taxa ou proporção calculada em relação ao número 100 (por cem), e é representada pelo símbolo %.
Consiste numa razão em que seu denominador é sempre 100.
Por exemplo, se num grupo de 100 pessoas existem 55 mulheres e 45 homens, podemos dizer que a porcentagem de mulheres é de 55%, enquanto a porcentagem de homens é 45%.
Etimologicamente, a palavra porcentagem se originou do latim per centum, que significa literalmente "por cento" ou "por cada centena".
A porcentagem é usada para comparar grandezas, calcular valores de lucro, desconto ou prejuízo e até mesmo taxas de juros.
Como calcular porcentagem
Na matemática, o cálculo de uma porcentagem pode ser feito através da regra de 3 simples, como nos exemplos abaixo.
Exemplo de cálculo de porcentagem
Para determinar o valor de 30% de 200, é preciso ter em mente que 100% é sempre igual ao total das unidades, ou seja, 200. O valor de unidades referentes a 30% é desconhecido, sendo este número "x" a resposta obtida com a regra de três.

Assim, 30% de 200 é 60.
Exemplo de problema com porcentagem
Imagine que uma professora possui 450 alunos e, nas provas finais, apenas 8% do total de seus alunos tiraram a nota máxima. Para saber quantos alunos tiraram a nota máxima, o cálculo da porcentagem deve ser feito da seguinte maneira:
Para descobrir o valor de 8% de 450, é preciso ter em mente que 100% é sempre igual ao total das unidades, ou seja, 450. O valor de unidades referentes a 8% é desconhecido. Então, o chamaremos de “X” para obter a reposta através da regra de três:
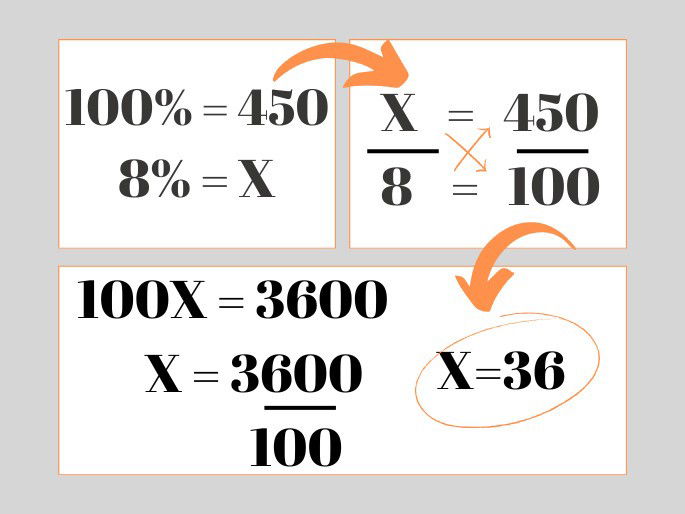
Assim, sabemos que 36 alunos tiraram a nota máxima nas provas finais, porque 8% de 450 = 36.
Saiba mais sobre regra de 3.
Para quê serve a porcentagem?
É uma medida matemática que é usada a comparar grandezas e determinar descontos, acréscimo de valores, quantidades, entre outros.
Todos esses cálculos estão presentes na vida cotidiana como, por exemplo, quando você ouve frases:
O preço da cesta básica aumentou 15% em relação ao ano passado.
A loja fará descontos de 30% a 70% durante o fim de semana.
A porcentagem também costuma ser muito utilizada para determinar comissões, ou seja, uma quantidade de dinheiro que é recebida ou paga por algum produto ou serviço.
É uma palavra frequentemente usada no contexto dos negócios, porque é a base do cálculo de lucros, prejuízos e descontos.
Exemplo:
Neste ano, os lucros da empresa aumentaram 15% em relação ao ano anterior.
Porcentagem para taxas de juros
A porcentagem também costuma ser usada para calcular as taxas de juros. Por exemplo, no caso de juros simples, se uma pessoa pede um empréstimo de R$ 1.000 com uma taxa de 10% de juros ao mês, e consegue pagar o empréstimo depois de um mês, terá que pagar R$ 1.100.
Ou seja, R$ 1.000 do dinheiro recebido, mais R$ 100 dos juros (100 é 10% de 1000).
Representações de porcentagem
A porcentagem é uma razão em que o denominador é sempre o número 100, por isso, variações de como pode ser representada. As representações podem ser percentual, decimal ou fracionária.
A representação percentual é a mais comum, utiliza o símbolo da porcentagem: %. Por exemplo: "30% de desconto", "15% de aumento dos impostos", "queda de 2% na bolsa de valores", entre outros.
Já a representação decimal pode ser mais facilmente reconhecida por possuir a vírgula, é a resposta da divisão por 100, como em 30:100 = 0,30, em 15:100 = 0,15 ou 2:100 = 0,02.
A representação fracionária é a que utiliza as frações como formato, como em 30/100, 15/100 e 2/100. É usada, por exemplo, se calcula porcentagem usando a regra de 3.
Origem do símbolo de porcentagem
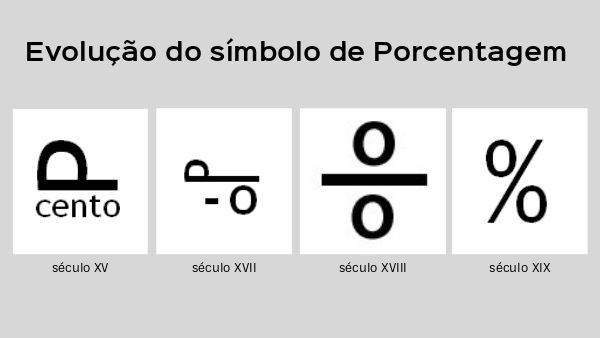
O atual símbolo usado para representar a porcentagem (%) é relativamente recente. Alguns documentos antigos mostram diferentes formas de indicar a porcentagem durante a Idade Média, por exemplo.
Inicialmente era usada a expressão "per cento" que, rapidamente, evoluiu para "per 100". Ao longo dos séculos foram surgindo outras maneiras de representar a porcentagem, como: pc-o, o/o e, finalmente, o %.
O que é o ponto percentual?
O ponto percentual (pp) consiste na unidade que representa a diferença entre porcentagens. Por exemplo, quando um desconto passa de 30% para 45% significa que houve um aumento de 50% no valor do desconto.
Algumas pessoas podem achar que o acréscimo é de 15%, visto ser essa a porcentagem acrescida aos 30% iniciais. No entanto, é preciso levar em consideração o fato de 15% representar a metade da porcentagem inicial (30%), ou seja, significa 50% deste número.
Assim, pode-se dizer que o resultado entre o aumento de 30% para 45% é se 15 pontos percentuais ou 50% de acréscimo.
Veja também: tipos de triângulos e formas geométricas.
Pratique mais sobre: