Cubo

Equipe do Significados

Criado e revisado pelos nossos especialistas

Um cubo é um sólido geométrico tridimensional, também chamado de hexaedro regular, formado por seis faces quadradas congruentes (ou seja, de mesmo tamanho). Todas as arestas do cubo têm o mesmo comprimento e seus ângulos internos são todos retos (90°).

Um exemplo de cubo no cotidiano são os dados de jogos. As características do cubo são:

• Faces: 6 faces quadradas.
• Vértices: 8 pontos onde as arestas se encontram.
• Arestas: 12 arestas, todas de mesmo comprimento.
• Simetria: é altamente simétrico, com múltiplos planos de simetria.

(imagem)

Planificação do cubo

(imagem)

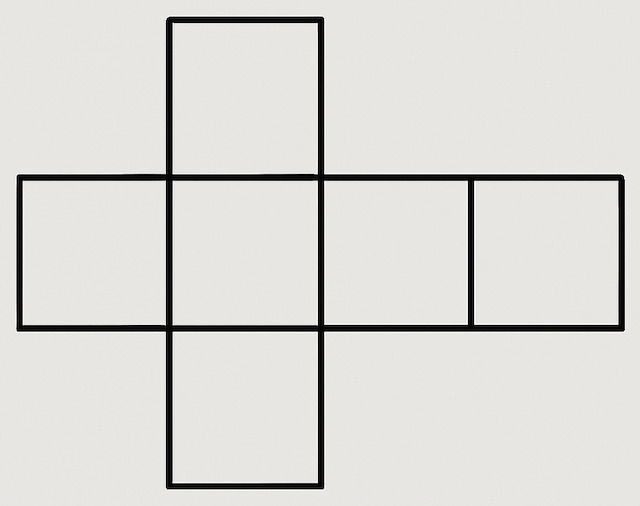
Para compreender melhor a estrutura de um cubo, é útil estudá-lo de forma plana. A planificação de um cubo é a representação bidimensional de suas faces, permitindo visualizar como elas se conectam no espaço tridimensional.

Um cubo possui 6 faces, ao "desdobrá-las", podemos formar várias configurações planas. Cada planificação consiste em seis quadrados dispostos de maneira que possam ser dobrados para recriar o cubo.

A planificação mais comum do cubo é uma cruz formada por cinco quadrados dispostos em linha e um adicional ligado ao centro. Existem outras planificações possíveis, desde que as seis faces estejam conectadas de forma que possam ser dobradas para formar o cubo.

Fórmulas do cubo e como calcular

As propriedades geométricas do cubo podem ser descritas matematicamente com fórmulas que relacionam seu comprimento de aresta (a²) com a área, o volume e a diagonal.

Área da superfície do cubo

A área total do cubo é a soma das áreas de todas as suas faces. Como cada face é um quadrado de lado a, a área de uma única face é

Exemplo: um cubo tem arestas de 4 cm. Qual é a área total de sua superfície?

• Comprimento da aresta (a) = 4 cm
• Área de uma face = a² = 4² = 16 cm²
• Área total = 6 x a² = 6 x 16 = 96 cm²

A área total do cubo é 96 cm².

Volume do cubo

O volume do cubo é o espaço tridimensional que ele ocupa. Para calcular, basta elevar o comprimento da aresta ao cubo (a³):

Exemplo: um cubo tem arestas de 3 cm. Qual é o volume?

• Comprimento da aresta (a) = 3 cm
• Volume = a³ = 3³ = 23 cm³

O volume do cubo é 27 cm³.

Comprimento diagonal do cubo

A diagonal do cubo é a linha que conecta dois vértices opostos, passando pelo interior da figura. Para calcular o comprimento da diagonal, usamos a fórmula:

Essa fórmula deriva do Teorema de Pitágoras aplicado no espaço tridimensional, considerando as dimensões do cubo.

Exemplo: um cubo tem arestas de 6 cm. Qual é o comprimento de sua diagonal?

• Comprimento da aresta (a) = 6 cm
• Diagonal = a√3 = 6√3 ≈10,39cm

O comprimento da diagonal do cubo é aproximadamente 10,39 cm.

Exercícios sobre cubo

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Leia também:

• Polígonos
• Tipos de triângulos
• Aresta
• Formas geométricas