Matemática

Cilindro

Equipe do Significados

Criado e revisado pelos nossos especialistas

O cilindro é uma figura geométrica formada por duas bases circulares congruentes e paralelas conectadas por uma superfície lateral curva. Esse formato está presente em objetos, como latas de refrigerante e rolos de papel.

Os elementos de um cilindro são:

Bases: os dois círculos paralelos e congruentes.
Raio (r): a distância do centro até a borda de cada base.
Altura (h): a distância perpendicular entre as duas bases.
Geratriz (g): a reta que conecta os pontos correspondentes nas bordas das bases ao longo da superfície lateral.

Ilustração de um cilindro verde em fundo cinza. — Cilindro.

Fórmulas do cilindro e como calcular

Para resolver problemas com cilindros, é essencial conhecer as principais fórmulas:

Área das bases do cilindro

Cada base é um círculo. A área de uma base é calculada por:

$A com b subscrito igual a pi espaço r ao quadrado$

$r espaço é espaço o espaço r a i o espaço d a espaço b a s e. espaço$
$pi espaço é espaço u m a espaço c o n s tan t e espaço parêntese esquerdo a p r o x i m a d a m e n t e espaço espaço 3 espaço vírgula 14 parêntese direito.$

Exemplo: cálculo da área da base de um cilindro com raio (r) de 5 cm.

$A com b subscrito igual a reto pi espaço reto r ao quadrado igual a 3 vírgula 14 espaço. espaço 5 à potência de 2 espaço fim do exponencial espaço igual a 3 vírgula 14 espaço. espaço 25 espaço igual a espaço 78 vírgula 5 cm$

Área lateral do cilindro

A área lateral corresponde à superfície curva que conecta as bases. Sua fórmula é:

$A com l subscrito igual a 2 reto pi rh$

r é o raio da base.
h é a altura do cilindro.

Exemplo: cálculo da área lateral de um cilindro com raio de 4 cm e altura de 10 cm.

$A com l subscrito igual a 2 reto pi rh espaço igual a 2 espaço. espaço 3 vírgula 14 espaço. espaço 4 espaço. espaço 10 espaço igual a espaço 251 vírgula 2 espaço cm$

Área total do cilindro

A área total é a soma da área lateral com as áreas das duas bases:

$A com t subscrito igual a A com l subscrito mais espaço 2 A com b subscrito igual a espaço 2 reto pi rh espaço mais 2 reto pi reto r ao quadrado$

$A com l subscrito igual a 2 reto pi rh espaço parêntese esquerdo área espaço lateral parêntese direito. espaço$
$A com b subscrito igual a reto pi reto r ao quadrado espaço parêntese esquerdo área espaço de espaço uma espaço base parêntese direito.$

Exemplo: cálculo da área total de um cilindro com raio de 3 cm e altura de 8 cm.

Cálculo da área da base: $A com b subscrito igual a reto pi reto r ao quadrado espaço igual a 3 vírgula 14 espaço. espaço 3 ao quadrado espaço igual a 3 vírgula 14 espaço. espaço 9 espaço igual a 28 vírgula 26 espaço cm ao quadrado$
Cálculo da área lateral: $A com l subscrito igual a 2 reto pi rh espaço igual a 2 espaço. espaço 3 vírgula 14 espaço. espaço 8 espaço igual a 150 vírgula 72 espaço cm ao quadrado$
Cálculo da área total: $A com t subscrito igual a A com l subscrito mais 2 A com b subscrito igual a espaço 150 vírgula 72 espaço mais espaço 2 espaço. espaço 28 vírgula 26 espaço igual a 150 vírgula 72 espaço mais espaço 56 vírgula 52 espaço igual a espaço 207 vírgula 24 espaço c m ao quadrado$

Volume do cilindro

O volume do cilindro é o espaço ocupado por ele, calculado como:

$V igual a reto pi reto r ao quadrado reto h$

r é o raio da base.
h é a altura do cilindro.

Exemplo: cálculo do volume de um cilindro com raio de 6 cm e altura de 12 cm.

$V igual a reto pi reto r ao quadrado reto h espaço igual a espaço 3 vírgula 14 espaço. espaço 6 ao quadrado espaço. espaço 12 espaço igual a espaço 3 vírgula 14 espaço. espaço 36 espaço.12 espaço igual a espaço 1356 vírgula 48 espaço cm ao cubo$

Planificação do cilindro

Cilindro roxo ao lado da mesma figura geométrica em versão planificada, em fundo amarelo. — Planificação do cilindro.

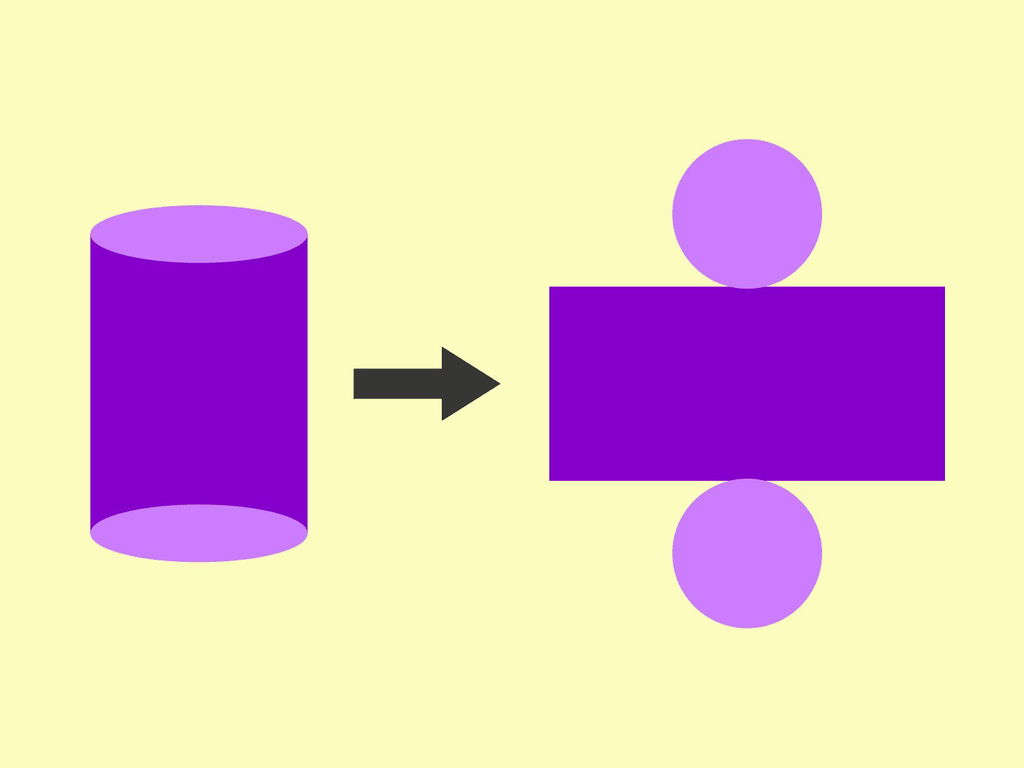
Ao planificar um cilindro, ele é transformado em uma figura bidimensional composta por:

Duas bases circulares.
Um retângulo, que representa a superfície lateral.

O comprimento do retângulo corresponde ao comprimento da circunferência da base $parêntese esquerdo 2 pi r parêntese direito$ e sua altura é igual à altura do cilindro (h).

Tipos de cilindro

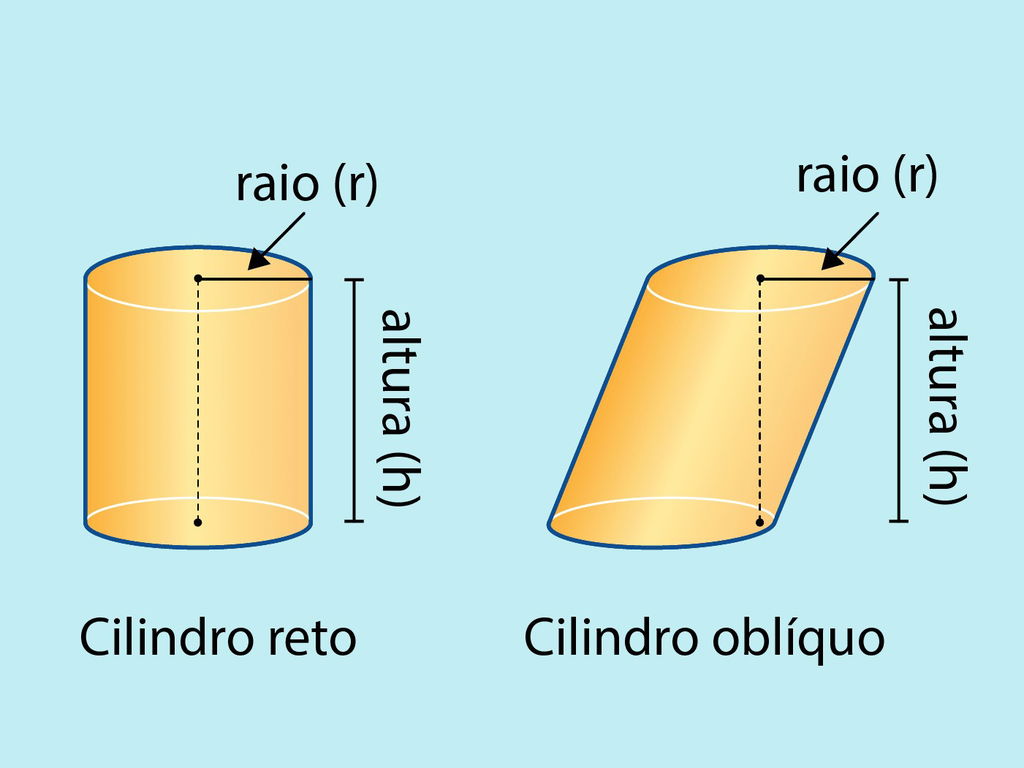
Os cilindros podem ser dos seguintes tipos:

Cilindro reto

O cilindro reto tem sua altura (h) sempre perpendicular às bases. Ou seja, a linha que conecta os centros das duas bases forma um ângulo de 90 graus com as superfícies dessas bases.

Este é o tipo mais comum de cilindro. Quando imaginamos um cilindro, geralmente estamos pensando nesse tipo, onde as bases são círculos idênticos e a superfície lateral é vertical em relação a essas bases.

Cilindro oblíquo

O cilindro oblíquo é um tipo de cilindro em que a altura não é perpendicular às bases, a linha que conecta os centros das bases forma um ângulo diferente de 90 graus com as superfícies dessas bases.

Dessa forma, o cilindro oblíquo tem uma aparência inclinada, como se as bases fossem "deslocadas" uma em relação à outra.

Cilindro equilátero

O cilindro equilátero é um tipo específico de cilindro reto em que a altura (h) é igual ao diâmetro da base (2r). Em outras palavras, no cilindro equilátero, o comprimento da altura é igual à medida da circunferência da base, o que cria uma relação única entre a altura e o raio.

Exercícios sobre cilindros

Exercício 1

Calcule a área total de um cilindro com raio de 5 cm e altura de 10 cm.

a) 78,5 cm²

b) 314 cm²

c) 471 cm²

d) 518 cm²

Exercício 2

Um cilindro tem raio r=7 cm e altura h=15 cm. Qual é o volume?

a) 2309,1 cm³

b) 3012 cm³

c) 2132 cm³

d) 2236 cm³

Exercício 3

Se um cilindro oblíquo tem raio r=4 cm e altura h=12cm. Qual é a área da base?

a) 48 cm²

b) 50,24 cm²

c) 48,24 cm²

d) 50,36 cm²

Exercício 4

Verifique se um cilindro de raio r=6 cm e altura h=12 cm é equilátero. Lembre que um cilindro é equilátero se sua altura for igual ao diâmetro (2r).

a) O cilindro é equilátero porque 2r =2. 6 =12 cm.

b) O cilindro não é equilátero porque 2r =2. 6 =12 cm.

c) O cilindro é equilátero porque 2r =2. 12 = 24 cm.

d) O cilindro não é equilátero porque 2r =2. 12 = 24 cm.

Exercício 5

Um cilindro tem diâmetro de 10 cm e altura de 20 cm. Calcule a área lateral do cilindro. Lembre que: $r espaço igual a espaço numerador d i â m e t o espaço sobre denominador 2 fim da fração.$

a) 650 cm²

b) 628 cm²

c) 528 cm²

d) 560 cm²

Veja também: