Exercícios sobre números racionais (questões resolvidas)
Os números racionais fazem parte do dia a dia. Frações e decimais são utilizados para descrever diversas situações. Pratique exercícios sobre estes números e tire suas dúvidas.
Questão 1
Em uma pizzaria, João pediu uma pizza e comeu dela. Em seguida, Ana comeu
da mesma pizza. Sabendo que a pizza estava inteira no início, qual fração da pizza ainda restou?
A)
B)
C)
D)
E)
Unificando os denominadores:
João comeu , que é equivalente a
.
Ana comeu .
Somando as partes consumidas:
Calculando a parte restante:
Como a pizza inteira equivale a :
Resposta Correta:
A)
Questão 2
Analise as afirmativas a seguir sobre o conjunto dos números racionais e identifique quais são verdadeiras e quais são falsas:
- Todo número racional pode ser escrito na forma de uma fração
, onde a e b são números inteiros e b ≠ 0.
- O conjunto dos números racionais é fechado para as operações de adição, subtração, multiplicação e divisão (exceto a divisão por zero).
- O número
pertence ao conjunto dos números racionais por poder ser aproximado por uma fração.
- Todo número inteiro é um número racional.
- O conjunto dos números racionais é denso, ou seja, entre dois números racionais quaisquer, sempre existe outro número racional.
Qual das alternativas a seguir está correta?
A) As afirmativas 1, 3 e 5 são verdadeiras.
B) As afirmativas 1, 2, 4 e 5 são verdadeiras.
C) As afirmativas 2, 3 e 4 são verdadeiras.
D) As afirmativas 1, 2, 3 e 5 são verdadeiras.
E) As afirmativas 3, 4 e 5 são verdadeiras.
Afirmativa 1: VERDADEIRA. Essa é a definição básica de um número racional. Por exemplo, 1,5 pode ser escrito como , como
, e assim por diante. Portanto, a afirmativa é verdadeira.
Afirmativa 2: VERDADEIRA. Quando você realiza qualquer uma dessas operações com dois números racionais, o resultado também será um número racional.
Afirmativa 3: FALSA. Embora possa ser aproximado por frações, como
ou
, ele nunca pode ser representado exatamente como uma fração. Isso é o que caracteriza um número irracional.
Afirmativa 4: VERDADEIRA. Todo número inteiro pode ser escrito como uma fração onde o denominador é igual a 1. Por exemplo, o número inteiro 5 pode ser representado como , e o número inteiro −7 pode ser representado como
.
Afirmativa 5: VERDADEIRA. Essa propriedade é verdadeira para os números racionais. Por exemplo, entre e
, podemos encontrar
ou
, e assim por diante. Isso é possível porque podemos sempre construir uma nova fração entre quaisquer duas frações existentes. Logo, a afirmativa é verdadeira.
Questão 3
Na expressão (onde o número 6 tem uma barra indicando dízima periódica), qual é a fração irredutível que representa este número racional?
A) 2456/999
B) 2450/999
C) 2456/990
D) 2211/900
E) 2211/990
Passo 1: Separar a parte inteira da parte decimal
Parte inteira: 2
Parte decimal: 0,456̅ (onde 6 é o algarismo que se repete infinitamente)
Passo 2: Converter a parte decimal (dízima periódica) em fração
Para converter 0,456̅ em fração, vamos usar o método padrão para dízimas periódicas:
Identificamos que temos 0,456̅ onde o algarismo 6 se repete
Nesse caso temos dois algarismos antes do período (4 e 5) e um algarismo no período (6)
Vamos chamar nossa dízima de x = 0,456̅
Multiplicamos por 1000 (10³) pois temos três algarismos no total: 1000x = 456,666... = 456,6̅
Multiplicamos por 10 (10¹) pois temos um algarismo no período: 10x = 4,566666... = 4,56̅
Agora fazemos a subtração: 1000x = 456,6̅ 10x = 4,56̅ 990x = 452,1
Portanto: x = 452,1/990 = 4521/9900
Passo 3: Adicionar a parte inteira
2 + 4521/9900 = (2 × 9900 + 4521)/9900 = 19800/9900 + 4521/9900 = 24321/9900
Passo 4: Simplificar a fração
Para simplificar 24321/9900, precisamos encontrar o MDC (máximo divisor comum) entre 24321 e 9900.
Usando o algoritmo de Euclides ou fatoração, encontramos que o MDC é 99.
Assim: 24321/9900 = (24321 ÷ 99)/(9900 ÷ 99) = 2211/900 = 2211/900
Portanto, a resposta correta é a alternativa d) 2211/900.
Questão 4
Na simplificação da expressão obtém-se:
A) 0,75
B) 1,2
C) 0,9
D) 0,45
E) 1,05
Vamos calcular o numerador:
Primeiro: 0,75 0,4 = 0,3
Depois:
Numerador: 0,3 - 0,09 = 0,21
Finalmente, dividimos pelo denominador:
Questão 5
João está planejando uma viagem de carro e precisa calcular seus gastos com combustível. Seu carro consome em média 12,5 km por litro de gasolina. O preço médio da gasolina na região é de R$ 5,85 por litro. João pretende viajar por uma distância de 320,4 km (ida) e retornar pelo mesmo caminho.
Durante a viagem, João planeja fazer duas paradas para refeições, gastando em média R$ 42,75 por refeição. Além disso, ele separou R$ 75,50 para eventuais despesas não previstas.
Considerando essas informações, calcule:
A) R$ 225,60
B) R$ 301,10
C) R$ 316,34
D) R$ 354,84
E) R$ 391,10
Distância total percorrida: 320,4 km (ida) + 320,4 km (volta) = 640,8 km
Quantidade de litros de combustível necessária: 640,8 km ÷ 12,5 km/L = 51,264 L
Gasto com combustível: 51,264 L × R$ 5,85/L = R$ 299,89
Gasto com refeições: 2 refeições × R$ 42,75 = R$ 85,50
Gastos adicionais: R$ 75,50
Subtotal de gastos previstos (combustível + refeições): R$ 299,89 + R$ 85,50 = R$ 385,39
Subtraindo os gastos adicionais, que não serão necessariamente utilizados: R$ 385,39 - R$ 75,50 = R$ 309,89
Adicionando 45% dos gastos adicionais como margem de segurança: R$ 309,89 + (R$ 75,50 × 0,45) = R$ 309,89 + R$ 44,95 = R$ 354,84
Portanto, João deverá reservar R$ 354,84 para sua viagem.
Aprenda mais sobre os números racionais.
-
Exercícios sobre porcentagem (com respostas explicadas)

-
Exercícios sobre produtos notáveis para estudar (resolvidos e explicados)

-
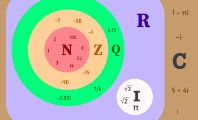
Conjuntos numéricos
-
Números racionais

-
Exercícios sobre equação do 1º grau (com questões resolvidas)

-
Exercícios sobre fórmula de Bhaskara para praticar (com gabarito)

-
Exercícios sobre sistemas lineares (com questões resolvidas e explicadas)

-
Exercícios sobre MMC e MDC (com questões explicadas)

-
Exercícios sobre frações (com questões respondidas e explicadas)

-
Exercícios de regra de três composta (com gabarito resolvido)

