Progressão Aritmética
O que é uma progressão aritmética:
Progressão Aritmética, também conhecida como P. A, é um tipo de sequência numérica estudada pela Matemática, onde cada termo ou elemento a contar a partir do segundo, é igual a soma do termo anterior com uma constante.
Neste tipo de sequência numérica, o número é sempre chamado de razão (representado pela letra r) e ele é obtido através da diferença de um termo da sequência pelo seu anterior.
Então, a partir do segundo elemento da sequência, os números serão todos resultantes da soma da constante com o valor do elemento anterior.
Por exemplo, a sequência 5,7,9,11,13,15,17 pode ser caracterizada como uma progressão aritmética, pois seus elementos são formados pela soma do seu antecessor com a constante 2.
Tipos de progressões aritméticas
Para compreender melhor este conceito, abaixo temos exemplos do que são considerados tipos de progressões aritméticas.
- (5,5,5,5,5...an) PA finita de razão 0
- (4,7,10,13,16...an...) PA infinita de razão 3
- (70,60,50,40,30...an) PA finita de razão -10
Nos três exemplos, observa-se que para se calcular a razão da PA, é preciso calcular a diferença entre um dos termos e o termo que o antecede, conforme a imagem abaixo mostra:
![]()
Fórmulas do termo geral e da soma de uma progressão aritmética
Neste sentido, a fórmula utilizada que caracteriza o termo geral de uma PA é representada desta forma:
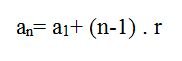
Onde, temos:
an = Termo geral
a₁ = Primeiro termo da sequência.
n = Número de termos da P.A. ou posição do termo numérico na P.A
r = Razão
Entretanto, se tivermos uma P.A finita qualquer, para somarmos os seus termos (elementos) chegaremos à seguinte fórmula para somarmos os n elementos de uma P.A finita.
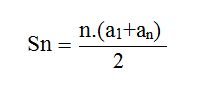
Onde, temos:
Sn = Soma dos n primeiros termos da PA
a₁ = Primeiro termo da PA
an = Ocupa a enésima posição na sequência
n = Posição do termo
Classificação das progressões aritméticas
No que diz respeito às classificações, as progressões aritméticas podem ser crescentes, decrescentes e constantes.
Uma PA será crescente quando sua razão (r) for positiva, ou seja, maior que zero (r > 0). A sequência numérica será crescente quando, cada termo a partir do segundo for maior que o antecessor. Ex: (1, 3, 5, 7, ...) é uma P.A crescente de razão 2.
Já a PA será decrescente se a sua razão (r) for negativa, ou seja,menor que zero (r < 0). A sequência numérica será decrescente quando, cada termo a partir do segundo for menor que o antecessor. Ex: (15, 10, 5, 0, -5 ...) é uma P.A decrescente de razão – 5.
A PA será constante quando sua razão for nula, ou seja, for igual a zero (r = 0). Todos os seus termos serão iguais. Ex: (2, 2, 2, ...) é uma P.A constante de razão nula.
Progressão aritmética e progressão geométrica
As progressões são estudadas pela matemática para definir números sequenciais reais, entretanto, existe uma diferença entre a progressão aritmética e a progressão geométrica.
Enquanto a progressão aritmética apresenta a sequência de números onde a diferenças numéricas entre um termo e seu antecedente é constante, na progressão geométrica a constante deriva do quociente deste termo e do seu antecessor.
Veja também: Progressão Geométrica.